Bulk synchronous parallel
The Bulk Synchronous Parallel (BSP) abstract computer is a bridging model for designing parallel algorithms. A bridging model "is intended neither as a hardware nor a programming model but something in between" [1]. It serves a purpose similar to the Parallel Random Access Machine (PRAM) model. BSP differs from PRAM by not taking communication and synchronization for granted. An important part of analysing a BSP algorithm rests on quantifying the synchronisation and communication needed.
BSP was developed by Leslie Valiant during the 1980s. The definitive article [1] was published in 1990.
Contents |
The model
A BSP computer consists of processors connected by a communication network. Each processor has a fast local memory, and may follow different threads of computation. A BSP computation proceeds in a series of global supersteps. A superstep consists of three ordered stages:
- Concurrent computation: Several computations take place on every participating processor. Each process only uses values stored in the local memory of the processor. The computations are independent in the sense that they occur asynchronously of all the others.
- Communication: At this stage, the processes exchange data between themselves.
- Barrier synchronisation: When a process reaches this point (the barrier), it waits until all other processes have finished their communication actions.
The figure below shows this in a diagrammatic form. The processes are not regarded as having a particular linear order (from left to right or otherwise), and may be mapped to processors in any way.
Communication
In many parallel programming systems, communications are considered at the level of individual actions: sending and receiving a message, memory to memory transfer, etc. This is difficult to work with, since there are many simultaneous communication actions in a parallel program, and their interactions are typically complex. In particular, it is difficult to say much about the time any single communication action will take to complete.
The BSP model considers communication actions en masse. This has the effect that an upper bound on the time taken to communicate a set of data can be given. BSP considers all communication actions of a superstep as one unit, and assumes all messages have a fixed size.
The maximum number of incoming or outgoing messages for a superstep is denoted by  . The ability of a communication network to deliver data is captured by a parameter
. The ability of a communication network to deliver data is captured by a parameter  , defined such that it takes time
, defined such that it takes time 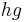 for a processor to deliver
for a processor to deliver  messages of size 1.
messages of size 1.
A message of length  obviously takes longer to send than a message of size 1. However, the BSP model does not make a distinction between a message length of
obviously takes longer to send than a message of size 1. However, the BSP model does not make a distinction between a message length of  or
or  messages of length 1. In either case the cost is said to be
messages of length 1. In either case the cost is said to be 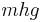 .
.
The parameter  is dependent on the following factors:
is dependent on the following factors:
- The protocols used to interact within the communication network.
- Buffer management by both the processors and the communication network.
- The routing strategy used in the network.
- The BSP runtime system.
A value for  is, in practice, determined empirically for each parallel computer. Note that
is, in practice, determined empirically for each parallel computer. Note that  is not the normalised single-word delivery time, but the single-word delivery time under continuous traffic conditions.
is not the normalised single-word delivery time, but the single-word delivery time under continuous traffic conditions.
Barriers
On most of today's architectures, barrier synchronization is often expensive, so should be used sparingly. However, future architecture developments may make them much cheaper. The cost of barrier synchronization is influenced by a couple of issues:
- The cost imposed by the variation in the completion time of the participating concurrent computations. Take the example where all but one of the processes have completed their work for this superstep, and are waiting for the last process, which still has a lot of work to complete. The best that an implementation can do is ensure that each process works on roughly the same problem size.
- The cost of reaching a globally consistent state in all of the processors. This depends on the communication network, but also on whether there is special-purpose hardware available for synchronizing, and on the way in which interrupts are handled by processors.
The cost of a barrier synchronization is denoted by 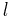 . In practice, a value of
. In practice, a value of 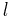 is determined empirically.
is determined empirically.
Barriers are potentially costly, but have a number of attractions. They do not introduce the possibility of deadlock or livelock, since barriers do not create circular data dependencies. Therefore tools to detect and deal with them are unnecessary. Barriers also permit novel forms of fault tolerance.
The Cost of a BSP algorithm
The cost of a superstep is determined as the sum of three terms; the cost of the longest running local computation, the cost of global communication between the processors, and the cost of the barrier synchronisation at the end of the superstep. The cost of one superstep for  processors:
processors:
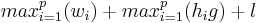 where
where 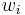 is the cost for the local computation in process
is the cost for the local computation in process  , and
, and 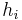 is the number of messages sent or received by process
is the number of messages sent or received by process  . Note that homogeneous processors are assumed here. It is more common for the expression to be written as
. Note that homogeneous processors are assumed here. It is more common for the expression to be written as 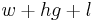 where
where  and
and  are maxima. The cost of the algorithm then, is the sum of the costs of each superstep.
are maxima. The cost of the algorithm then, is the sum of the costs of each superstep.
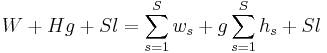 where
where  is the number of supersteps.
is the number of supersteps.
 ,
,  , and
, and  are usually modelled as functions, that vary with problem size. These three characteristics of a BSP algorithm are usually described in terms of asymptotic notation, e.g.
are usually modelled as functions, that vary with problem size. These three characteristics of a BSP algorithm are usually described in terms of asymptotic notation, e.g. 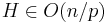 .
.
Extensions and uses
BSP has been extended by many authors to address concerns about BSP's unsuitability for modelling specific architectures or computational paradigms. One example of this is the decomposable BSP model. The model has also been used in the creation of a number of new programming languages --- including BSML (Bulk Synchronous Parallel ML) --- and programming models --- including BSPLib[2], Apache Hama, MapReduce, and Pregel[3].
See also
- Computer cluster
- Concurrent computing
- Concurrency
- Dataflow programming
- Grid computing
- Parallel computing
- ScientificPython
- LogP machine
References
External links
- D.B. Skillicorn, Jonathan Hill, W. F. McColl, Questions and answers about BSP (1996)
- BSP Worldwide
- BSP related papers
- WWW Resources on BSP Computing
- (French) Bulk Synchronous Parallel ML ((English) official website)